梯子图形的面积怎么求-梯子图形的面积怎么求公式

如怎样证明勾股定理？学生通过自学，中等以上的学生基本掌握，这时能激发学生的表现欲2教师引导学生按照要求进行拼图，观察并分析 1这两个图形有什么特点？2你能写出这两个图形的面积吗？ 3如何运用勾股定理？是否还有其他形式？ 这时教师组织学生分组讨论，调动全体学生的积极性，达到人人参与的效果，接着全班。

梯形的体积=上底+下底×高÷2×总长度梯形的体积计算公式是梯形的体积=上底+下底×高÷2×总长度平行的两边叫做梯形的底边，较长的一条底边叫下底，较短的一条底边叫上底，另外两边叫腰，夹在两底之间的垂线段叫梯形的高。

梯形的面积公式推导过程及其相关知识如下1假设梯形的上底为a，下底为b，高为h梯形的面积为5+10×6÷2=455+10×6÷2=45平方单位因此，梯形的面积公式为梯形面积=上底+下底×高÷22梯形具有两个相等的角，两个互补的角和两个对角线这种形状最早在古希腊数学家欧。

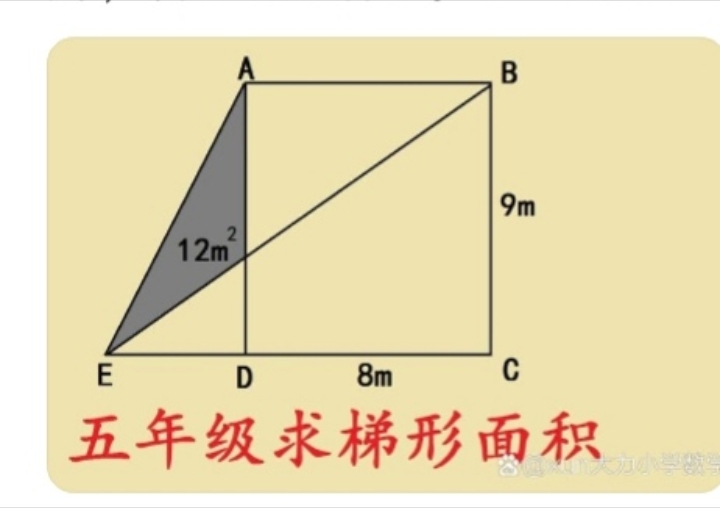
将图形转化为边在格线上的图形，以便于计算图形面积，体现了数形结合的思想学生会想到用quot数格子quot的方法，这种方法虽然简单易行，但对于下一步探索一般直角三角形并不适用，具有局限性因此教师应引导学生利用quot割quot和quot补quot的方法求正方形C的面积，为下一步探索复杂图形的面积做铺垫 突破等腰直角三角形的束缚，探索。

每个直角三角形的面积为ab2中间懂得小正方形边长为ba，则面积为ba2于是便可得如下的式子4×ab2+ba2=c2化简后便可得a2+b2=c2亦即c=a2+b212赵爽的这个证明可谓别具匠心，极富创新意识他用几何图形的截割拼补来证明代数式之间的恒等关系，既具。