一元三次方程韦达定理公式解法:一元三次方程韦达定理公式解法视频

一元三次方程韦达定理的完整公式如下根的和x_1 + x_2 + x_3 = fracba$根的积的和x_1x_2 + x_2x_3 + x_1x_3 = fracca$三根的积x_1x_2x_3 = fracda$这三个公式共同构成了一元三次方程韦达定理的完整表述，它们揭示了方程的根与其系数之间的直接。

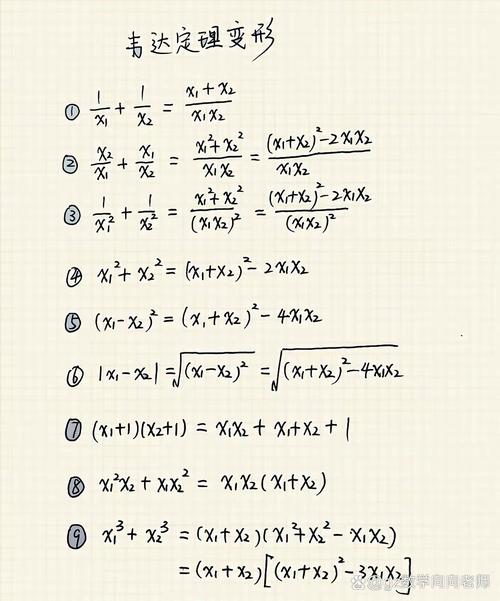
一元三次方程韦达定理是设三次方程为ax^3+bx^2+cx+d=0 三个根分别为x1，x2，x3，则方程又可表示为axx1xx2xx3=0 即ax^3ax1+x2+x3x^2+ax1*x2+x2*x3+x3*x1ax1*x2*x3=0 对比原方程ax^3+bx^2+cx+d=0 可知 x1+x2+x3=ba x1*x2+x2*x3+。

一元三次方程定理为x1x2x3=da韦达定理说明了一元二次方程中根和系数之间的关系法国数学家弗朗索瓦·韦达在著作论方程的识别与订正中建立了方程根与系数的关系，提出了这条定理由于韦达最早发现代数方程的根与系数之间有这种关系，人们把这个关系称为韦达定理学数学技巧 1抓住课堂。

一元三次方程求根公式通过归纳思维推导，不同于一元二次方程的直接求解方法通常的演绎思维无法直接求解一元三次方程，而需要将一般形式转化为特殊形式对于方程x^3+px+q=0，其解的形式为x=A^13+B^13将x=A^13+B^13两边立方得x^3=A+B+3AB^13A^1。

解析如下设三次方程为ax^3+bx^2+cx+d=0 三个根分别为x1，x2，x3，则方程又可表示为axx1xx2xx3=0，即ax^3ax1+x2+x3x^2+ax1*x2+x2*x3+x3*x1ax1*x2*x3=0 对比原方程ax^3+bx^2+cx+d=0 可知 x1+x2+x3=ba x1*x2+x2*x3+x3*x1=ca x。

1解法思想 三次方程是未知项总次数最高为3的整式方程，其解法思想是通过配方和换元，使三次方程降次为二次方程而韦达定理说明了一元二次方程中根和系数之间的关系，法国数学家弗朗索瓦·韦达在著作论方程的识别与订正中建立了方程根与系数的关系，提出了这条定理一元三次方程求根公式用通常的。